2. 中国石油青海油田公司, 甘肃敦煌 736202
2. PetroChina Qinghai Oilfield Company, Dunhuang 736202, China
国外一些学者研究发现[1-4], 一个含油气盆地中, 勘探早期发现的总是大中型油气藏, 中后期主要以发现中小型油气藏为主, 并且具有油气藏储量规模越大, 其数量越少, 油气藏储量规模越小, 其数量越多的特征。油气藏数量与其储量规模之间符合幂函数关系, 也即油气藏分布具有分形特征。油气藏分布的分形特征是指累积油气藏数量与其储量规模之间具有幂函数关系[5]。不少国内学者将该理论应用于未发现油气藏数量和储量资源的预测研究, 并取得良好效果[6-12]。但是这一理论实际应用中有两个根本性问题没有解决。一个问题是分形维数的地质含义, 目前有两类完全相反的解释:一些学者[8-9]认为, 分形维数越大, 勘探潜力越大, 而分形维数越小, 勘探潜力越小; 也有学者[11-12]认为, 分形维数是勘探成熟度的反映, 分形维数越小, 勘探潜力越大, 分形维数越大, 勘探潜力越小。另一个问题是油气藏储量规模与其数量之间具有分形特征而不具有其他分布特征的原因。对这两个问题进行系统理论研究, 目前国内外尚未见有公开发表的信息。笔者采用成藏动力学与非平衡态热力学相结合方法, 揭示油气藏分形特征形成的动力学机制及适用条件, 从理论上回答这两个问题。
1 油气运移有效驱动力及速度为了使问题分析简化, 在温度压力变化范围不大情况下, 假定油气流体密度和黏度参数近似不变。如果研究对象是常压盆地, 地层水中呈离散(或连续)状运移的油珠, 由于油与水的密度不相等, 则油珠不仅受重力和浮力作用, 还要受到毛细管阻力作用[13]。如果研究对象为超压盆地时, 还要受到剩余压力作用, 则油珠所受驱动力可表示为
| $ {P_{\rm{d}}} = \left[ {\left( {{\rho _{\rm{w}}}g + {P_{\rm{r}}} - {\rho _{\rm{o}}}g} \right]{h_{\rm{o}}}\sin \theta = \left( {{\rho _{{\rm{ow}}}}g + {P_{\rm{r}}}} \right){h_{\rm{o}}}\sin \theta } \right.. $ | (1) |
式中, Pd为油气运移驱动力, MPa; Pr为垂向剩余压力梯度, MPa/m;θ为油气运移方向与水平方向夹角, (°); g为重力加速度, m/s2; ρw为地层水密度, g/cm3; ho为油珠高度, m;ρo为油密度, g/cm3; ρow为油水密度差, g/cm3。式(1)为油气运移驱动力公式, 由两项组成, 第一项为浮力与重力的合力, 称为净浮力; 第二项称为剩余压力。对于常压盆地, 第二项剩余压力为零, 以净浮力为运移驱动力; 对于超压盆地, 第二项剩余压力不为零, 以净浮力与剩余压力之和为其运移驱动力。在常见超压盆地中, 油气净浮力在其数值上要比剩余压力小一个数量级[13]。
油气运移阻力主要是储层毛细管力, 决定于孔喉结构、流体性质、流体界面张力和润湿角等, 可以用排驱压力参数来表示[14-15]。根据油气运移驱动力公式(1), 只有油气运移驱动力大于排驱压力时, 油气流体才能驱替孔隙中地层水而充注油气。因此, 实际油气运移有效驱动力可表示为
| $ {P_{\rm{e}}} = \left( {{\rho _{{\rm{ow}}}}g + {P_{\rm{r}}}} \right){h_{\rm{o}}}\sin \theta - {P_{\rm{c}}}. $ | (2) |
式中, Pe为油气运移有效驱动力, MPa; Pc为排驱压力, MPa。式(2)为油气运移有效驱动力公式。对于常压盆地而言, 由于油气运移驱动力为净浮力, 属于弱运移驱动力; 对于超压盆地而言, 由于油气运移驱动力为净浮力与剩余压力之和, 属于强运移驱动力。油气运移有效驱动力, 实际上就是油气运移驱动力减去储层排驱压力后的净油气运移驱动力。例如, 对于具有高排驱压力的致密储层而言, 尽管剩余压力可能较高, 但克服运移路径高排驱压力后, 实际上油气运移有效驱动力则会变小, 也属于较弱油气运移有效驱动力。
依据油气运移有效驱动力公式(2)和Darcy方程, 则油气运移速度为
| $ v = \frac{k}{{{\mu _{\rm{o}}}}}\left[ {\left( {{\rho _{{\rm{ow}}}}g + {P_{\rm{r}}}} \right)\sin \theta - {P_{\rm{g}}}} \right]. $ | (3) |
式中, Pg为排驱压力梯度, MPa/m; v为油气运移速度, m/Ms; μo为地层原油黏度, mPa·s; k为渗透率, μm2。油气运移速度由3项组成:第一项为净浮力驱动下运移速度, 称之为净浮力速度; 第二项为剩余压力驱动下速度, 称为剩余压力速度; 第三项为排驱压力耗损速度, 称为排驱压力耗损速度。对于常压盆地, 第二项剩余压力梯度为零, 以净浮力速度和排驱压力耗损速度二者之和为其运移速度; 对于超压盆地, 第二项剩余压力梯度不为零, 以净浮力速度、剩余压力速度和排驱压力耗损速度三项之和为其运移速度。
2 油气运移最小能耗率原理先做一定义:盆地充填物孔隙(裂)及其中流体组成的系统, 称之为盆地流体系统。依流体运移状态的不同, 可分为以连续状运移方式的盆地水系统和呈离散(或连续)状油珠或气泡方式运移的盆地油气系统。呈离散(或连续)状运移的油气, 以盆地水系统中呈连续状运移的地层水为依托载体。可认为, 盆地流体系统由盆地水系统和盆地油气系统这两个子系统组成。
盆地油气成藏过程是一个复杂的非线性动力学过程, 同时也是一个热力学能量耗散的非平衡过程[16]。一般地, 一个系统处于外部恒定驱动力作用下, 经过一定时间以后, 系统将会达到与这一外部恒定驱动力相适应的在宏观上不随时间变化的稳定状态, 称之为非平衡定态, 简称定态。根据非平衡态热力学理论[17-18], 在弱油气运移有效驱动力作用下, 盆地油气系统将处于线性非平衡态区, 简称为近平衡态区。盆地油气系统将趋于与弱油气运移有效驱动力相适应的具有非均质结构定态, 盆地油气系统熵产生将趋于最小值, 并遵从最小熵产生原理。在强油气运移有效驱动力作用下, 盆地油气系统将处于非线性非平衡态区, 简称为非平衡态区。处于非平衡态区的盆地油气系统的熵产生却不一定取最小值, 而是偏离最小值, 最小熵产生原理将不再成立[19]。
处于近平衡态盆地油气系统, 将趋于与弱油气运移有效驱动力相适应具有非均质结构定态。这一油气流体分布非均质结构定态格局维持, 也是一个物质流和能量流的能量耗散过程, 并遵从最小熵产生原理。因此在弱油气运移有效驱动力作用下, 油气流体运移过程中的能量耗散状况控制着油气流体分布的非均质结构定态格局。
在实际应用中, 可认为熵产生函数等价于能耗率函数, 最小熵产生原理也等价于最小能耗率原理[20-21]。盆地油气系统处于与弱油气运移有效驱动力相适应的油气分布非均质结构定态时, 盆地油气系统能量流与物质流的能耗率可表示为
| $ \varphi = {\varphi _{\rm{e}}} + {\varphi _{\rm{m}}}. $ | (4) |
式中, φe为能量流的能耗率函数, 表示单位时间单位体积内能量流所耗散的能量, J/(m3·s); φm为质量流的能耗函数, 表示单位时间单位体积内质量流所耗散的能量, J/(m3·s); φ为单位时间单位体积内质量流与物质流所耗散总能量, J/(m3·s)。它们是由油气运移这一不可逆过程引起的, 油气运移能量流通过动量传输实现, 油气运移物质流通过质量传输实现[22]。根据广义流与广义力构造能耗率函数的原则[19], 油气运移能量流定义为动量与速度之积, 为其广义流。流速梯度为动量传输的广义力, 并从高速区流向低速区, 则能量流的能耗率可表示为
| $ {\varphi _{\rm{e}}} = - \left( {{\rho _{\rm{o}}}{v^2}} \right)\frac{{\partial v}}{{\partial l}}. $ | (5) |
式中, l为油气运移方向, m。物质流可定义为油气运移速度与密度乘积, 反映单位时间内传输质量, 为其广义流。油气运移有效驱动力梯度为质量传输的广义力, 则质量流的能耗率可表示为
| $ {\varphi _{\rm{m}}} = \left( {v{\rho _{\rm{o}}}} \right)\left( {\frac{1}{{{\rho _{\rm{o}}}}}\frac{{\partial {P_{\rm{e}}}}}{{\partial l}}} \right). $ | (6) |
根据最小能耗率原理, 盆地油气系统处于与弱油气运移有效驱动力相适应油气分布的非均质结构定态时, 盆地油气系统能耗率将趋于最小值。根据式(4), 则盆地油气系统总能耗率为
| $ \begin{array}{*{20}{c}} {{\mathit{\Phi }_{\min }} = \iiint\limits_V {\varphi {\text{d}}V} = \iiint\limits_V {\left( {{\varphi _{\text{e}}} + {\varphi _{\text{m}}}} \right){\text{d}}V} = \iiint\limits_V {\left[ { - \left( {{\rho _{\text{o}}}{v^2}} \right)\frac{{\partial v}}{{\partial l}} + } \right.}} \\ {\left. {\left( {v{\rho _{\text{o}}}} \right)\left( {\frac{1}{{{\rho _{\text{o}}}}}\frac{{\partial {P_{\text{e}}}}}{{\partial l}}} \right)} \right]{\text{d}}V = \iiint\limits_V {v\left[ { - \frac{\partial }{{\partial l}}\left( {{\rho _{\text{o}}}\frac{{{v^2}}}{2}} \right) + \frac{{\partial {P_{\text{e}}}}}{{\partial l}}} \right]{\text{d}}V}.} \end{array} $ | (7) |
式中, Φmin为盆地油气系统能耗率最小值, 表示盆地油气系统处于定态时, 单位时间内系统耗散总能量, J/s; V为盆地油气系统油气流体总体积, 也即油气藏累加总储量, 104m3。体积分中括号内有两项, 第一项是油气流体动压强梯度, 第二项等同于油气流体静压强梯度。这二项之和代表油气运移驱动能量大小, 由于油气运移速度极小, 第一项可忽略不计。将油气运移有效驱动力公式(2)和油气运移速度公式(3)带入公式(7), 根据积分中值定律, 可将公式(7)简化为
| $ \begin{gathered} {\mathit{\Phi }_{\min }} = \iiint\limits_V {v\frac{{\partial {P_{\text{e}}}}}{{\partial l}}{\text{d}}V} = \iiint\limits_V {\frac{k}{{{\mu _0}}}{{\left[ {\left( {{\rho _{{\text{ow}}}}g + {P_{\text{r}}}} \right)\sin \theta - {P_{\text{g}}}} \right]}^2}{\text{d}}V} \hfill \\ = VW. \hfill \\ \end{gathered} $ | (8) |
其中
| $ W = \frac{k}{{{\mu _{\rm{o}}}}}{\left[ {\left( {{\rho _{{\rm{ow}}}}g + {P_{\rm{r}}}} \right)\sin \theta - {P_{\rm{g}}}} \right]^2}. $ | (9) |
式中, W为平均单位体积油气流体所受有效驱动功率, 简称为油气运移有效驱动功率, J/(s·m3)。式(8)称为油气运移最小能耗率原理。从油气运移有效驱动功率公式(9)可看出, 油气运移有效驱动功率大小取决于5个因素, 即净浮力梯度(ρowg)、剩余压力梯度(Pr)、排驱压力梯度(Pg)、油气运移方向(θ)和流度(k/μo)。油气运移最小能耗率原理揭示了这5个因素与油气藏总储量(V)间关系规律。
油气运移最小能耗率原理(式(8))表明, 在弱油气运移有效驱动力作用下, 油气运移能耗率将趋于最小值, 也即油气运移具有“惰性”特征, 油气运移将选择一种“低耗高效”方式进行。显然, 以断层垂向运移或以储层中相对高渗层带侧向就近运移的路径是油气最可能运移路径, 因为二者具有最小能耗率。
油气运移最小能耗率原理也表明, 在弱油气运移有效驱动力作用下, 由于盆地油气系统最小能耗率(Φmin)为一常数, 盆地油气系统油气藏累加总储量(V), 与油气运移有效驱动功率(W)成反比关系。当油气成藏要素相同情况下, 油气运移有效驱动功率(W)越大, 则油气藏总规模(V)越小; 相反, 油气运移有效驱动功率(W)越小, 则油气藏总规模(V)越大。
需要说明的是, 地层倾角对油气成藏影响很大。当其他4个成藏要素不变情况下, 根据油气运移有效驱动功率公式(9)和油气运移最小能耗率原理公式(8), 如果油气运移方向与水平方向夹角减小, 油气运移有效驱动功率将大幅减小(近似与sin2θ成正比), 导致油气藏规模大幅增大。
3 油气藏分形特征形成机制根据油气运移最小能耗率原理(式(8)), 在盆地油气系统处于与弱油气运移有效驱动力相适应定态时, 如果盆地油气系统油气藏总体积V由N个不同规模储量的油气藏(x)组成,考虑到盆地中油气藏储量之间的悬殊性, 这N个油气藏储量平均值取加权几何平均值,
| $ {m^N} = {\left( {{x_1}} \right)^{{n_1}}}{\left( {{x_2}} \right)^{{n_2}}} \cdots {\left( {{x_i}} \right)^{{n_i}}}. $ | (10) |
式中, m为油气藏储量的加权几何平均值, 104 m3; x1, x2, …, xi为油气藏储量规模, 104 m3, i为油气藏储量规模序号; n1, n2, …, ni为与之相对应的油气藏个数。对式(10)两边取对数, 即
| $ N\ln m = {n_1}\ln {x_1} + {n_2}\ln {x_2} + \cdots + {n_i}\ln {x_i} = \sum\limits_1^i {{n_i}\ln {x_i}} . $ | (11) |
对于连续油气藏储量x, 其加权几何平均值与式(11)类似, 应有
| $ \ln m = \int_a^b {f\left( x \right)\ln x{\rm{d}}x} . $ | (12) |
式中, f(x)为盆地内N个油气藏储量分布概率密度函数; x为油气藏储量变量, 104 m3; a、b分别为油气藏储量x的上、下限值, 104 m3。对于盆地内N个油气藏储量分布概率密度函数f(x), 则有
| $ \int_a^b {f\left( x \right){\rm{d}}x} = 1. $ | (13) |
依据油气运移最小能耗率原理(式(8)), 盆地油气系统能耗率取得最小值, 也意味着盆地内N个油气藏分布的信息熵取得最大值,
| $ - \int_a^b {f\left( x \right)\ln f\left( x \right){\rm{d}}x} = \max . $ | (14) |
那么在方程(14)约束下, 何种类型油气藏储量分布概率密度函数f(x), 使盆地油气系统内油气藏储量分布的信息熵值最大(也即能耗率最小), 这是一个泛函数的求极值问题, 采用拉格朗日方法进行求解[23]。联立式(14)、(13)和(12), 构造一个新函数
| $ \begin{array}{l} H = - \int_a^b {f\left( x \right)\ln f\left( x \right){\rm{d}}x} + {s_1}\left[ {\int_a^b {f\left( x \right){\rm{d}}x} - 1} \right] + \\ {s_2}\left[ {\int_a^b {f\left( x \right)\ln x{\rm{d}}x} - \ln m} \right]. \end{array} $ | (15) |
式中, s1和s2为待定常数。可看出, H是油气藏储量分布概率密度函数f(x)的函数。求H对f(x)偏微商, 并令其为零, 整理可得
| $ f\left( x \right) = \exp \left( { - 1 + {s_1}} \right){x^{{s_2}}}. $ | (16) |
为了使式(16)简化, 假定式(13)中油气藏储量x最小值为1, 在积分上限b处f(x)函数值为0, 再联立式(12)和(13), 可消去未知数s1和s2, 求得油气藏储量分布概率密度函数为
| $ f\left( x \right) = \frac{1}{{\ln m}}{x^{\left( { - 1 - \frac{1}{{\ln m}}} \right)}}. $ | (17) |
根据油气运移最小能耗率原理(式(8)), 由N个油气藏储量构成的总储量V可表示为
| $ mN = \frac{{{\mathit{\Phi }_{\min }}}}{W}. $ | (18) |
将式(18)代入式(17)得
| $ f\left( x \right) = \frac{1}{{\ln \left( {\frac{{{\mathit{\Phi }_{\min }}}}{{NW}}} \right)}}{x^{\left( { - 1 - \frac{1}{{\ln \left( {\frac{{{\mathit{\Phi }_{\min }}}}{{NW}}} \right)}}} \right)}}. $ | (19) |
式(19)为油气藏储量分布概率密度函数公式, 为幂函数分布, 具有分形结构。
可见, 在弱油气运移有效驱动力作用下, 处于近平衡态区盆地油气系统, 油气运移遵守油气运移最小能耗率原理, 盆地油气藏储量分布才具有分形特征; 相反, 强油气运移有效驱动力作用下, 处于非平衡态区盆地油气系统, 油气运移最小能耗率原理不再成立, 盆地油气藏分布则不具有分形特征。因此弱油气运移有效驱动力作用下的油气运移最小能耗率原理, 是盆地油气藏储量分布具有分形特征的动力学机制及适用条件。
再对式(19)两边取对数
| $ \ln f\left( x \right) = \ln \left( {\frac{1}{{\ln \left( {\frac{{{\mathit{\Phi }_{\min }}}}{{NW}}} \right)}}} \right) + \left( { - 1 - \frac{1}{{\ln \left( {\frac{{{\mathit{\Phi }_{\min }}}}{{NW}}} \right)}}} \right)\ln x. $ | (20) |
显然, 在双对数坐标中式(20)反映油气藏储量分布概率密度函数与油气藏储量之间呈线性关系, 则此直线斜率为
| $ D = 1 + \frac{1}{{\ln \left( {\frac{{{\mathit{\Phi }_{\min }}}}{{NW}}} \right)}}. $ | (21) |
式中, D为直线段斜率, 称为油气藏储量分布的分形维数公式。至此, 从理论上证明了, 只有在弱油气运移有效驱动力作用下, 处于近平衡态区盆地油气系统, 油气藏分布才具有分形特征。
油气藏储量分布的分形维数公式(21)也揭示了分形维数D地质含义:如果盆地油气系统中油气藏数量(N)为一定值情况下, 由于Φmin为一常数, 分形维数D只与油气运移有效驱动功率(W)有关, 而与油气勘探潜力没有直接关系。
这样, 也就从理论上回答本文在引言中提出的两个问题, 即分形维数D地质含义和为什么油气藏分布具有分形特征的问题。
需要说明一点, 在实际工作中多用油气藏累积数量与储量间关系进行油气藏储量分形特征研究, 而油气藏储量分布概率密度函数公式(19)为一个幂函数。由于幂函数的积分仍然是幂函数, 油气藏累积数量与储量关系也服从幂函数关系。
4 应用实例饶阳凹陷位于渤海湾盆地中西部, 为一个东断西超的箕状凹陷, 也是一个油气最富集凹陷。根据文献[9]提供的储量数据(表 1), 凹陷内已发现201个油藏, 其中前古近系发现16个油藏, 沙河街组发现油藏88个, 东营组发现油藏70个, 新近系发现27个。由于沙河街组属于超压系统[24-25], 油气运移驱动力为净浮力与剩余压力之和, 在强油气运移有效驱动力作用下, 沙河街组油气系统能耗率偏离最小值, 系统处于非平衡态区, 油气运移最小能耗率原理不再成立。因此沙河街组油气藏分布不符合分形特征, 不能用于未发现油气藏储量资源的预测研究。
| 表 1 饶阳凹陷不同层位油藏规模及累积油藏个数[9] Table 1 Reserves scale and reservoir accumulated number of different layers in Raoyang Sag |
新近系和东营组为常压系统, 油气运移驱动力为净浮力。根据油气运移有效驱动力公式(2), 属于弱油气运移有效驱动力。在弱油气运移有效驱动力作用下, 新近系和东营组油气系统将处于近平衡态附近, 油气运移遵守最小能耗率原理, 油气藏分布符合幂函数分布, 具有分形特征, 可以用于未发现油气藏储量资源的预测研究。
油气藏储量分布的分形维数公式表明, 分形维数D近似反映油气运移有效驱动功率。反过来, 只要知道油气藏储量分布的分形维数D, 就可利用式(21)求得油气运移有效驱动功率。依照表 1中油气藏储量规模分级和相应油藏累积个数, 对新近系和东营组油藏累积个数与储量规模数据进行分形统计表明, 新近系和东营组油藏储量分布均具有很好分形特征。新近系油藏储量分布分形维数D1为1.29(图 1(a)), 东营组油藏储量分布分形维数D2为1.23(图 1(b))。
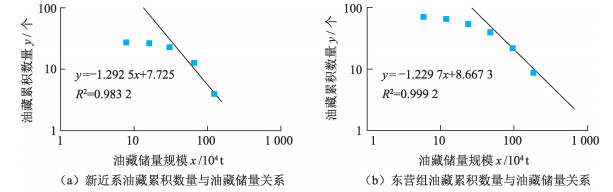
|
图 1 油藏累积数量与油藏储量规模关系 Fig.1 Relationship between reservoir accumulated number and reserves scale |
根据油气藏储量分布分形维数公式(21), 新近系与东营组油藏储量分布的分形维数之比为
| $ \frac{{{D_1}}}{{{D_2}}} = \frac{{1 + \frac{1}{{\ln \left( {\frac{{{\mathit{\Phi }_1}}}{{{N_1}{W_1}}}} \right)}}}}{{1 + \frac{1}{{\ln \left( {\frac{{{\mathit{\Phi }_2}}}{{{N_2}{W_2}}}} \right)}}}}. $ | (22) |
式中, D1、Φ1、N1和W1分别为新近系储量分布分形维数、最小能耗率、油藏总数量和油气运移有效驱动功率; D2、Φ2、N2和W2分别为东营组储量分布分形维数、最小能耗率、油藏总数量和油气运移有效驱动功率。再将式(22)化简, 可得新近系与东营组油气运移有效驱动功率之比为
| $ \frac{{{W_1}}}{{{W_2}}} = \frac{{{\mathit{\Phi }_1}{N_2}{{\rm{e}}^{\frac{1}{{{D_2} - 1}}}}}}{{{\mathit{\Phi }_2}{N_1}{{\rm{e}}^{\frac{1}{{{D_1} - 1}}}}}}. $ | (23) |
式中, 如果新近系和东营组油气系统能耗率最小值接近(Φ1≈Φ2), 经济界限之上的油藏数量接近(N1≈N2), 则将新近系和东营组油藏分布的分形维数(D1=1.29, D2=1.23)带入式(23), 可求得新近系与东营组油气运移有效驱动功率之比为2.46。
5 结论(1) 在弱油气运移有效驱动力作用下, 处于近平衡态区盆地油气系统, 油气运移遵守油气运移最小能耗率原理, 盆地油气藏分布具有分形特征; 相反, 强油气运移有效驱动力作用下, 处于非平衡态区盆地油气系统, 油气运移最小能耗率原理不再成立, 盆地油气藏分布则不具有分形特征。弱油气运移有效驱动力作用下的油气运移最小能耗率原理, 是盆地油气藏分形特征形成的动力学机制及适用条件。
(2) 油气藏储量分布的分形维数公式, 揭示了分形维数D地质含义。如果盆地油气系统中油气藏数量为一定值情况下, 由于Φmin为一常数, 分形维数D就只与油气运移有效驱动功率有关, 而与油气勘探潜力没有直接关系。分形维数D近似反映油气运移有效驱动功率。油气运移有效驱动功率越大, 分形维数就越大; 而油气运移有效驱动功率越小, 分形维数也越小。
(3) 油气运移最小能耗率原理表明, 在弱油气运移有效驱动力作用下, 油气运移具有“惰性”特征, 油气运移将选择一种“低耗高效”方式进行。以断层垂向运移或以储层中相对高渗层带侧向就近运移的路径是油气最可能运移路径, 因为二者具有最小能耗率。
(4) 油气运移最小能耗率原理也表明, 油气运移有效驱动功率越大, 油气藏规模则越小; 相反, 油气运移有效驱动功率越小, 油气藏规模则越大。地层倾角对油气成藏影响很大。根据油气运移有效驱动功率公式和油气运移最小能耗率原理公式, 如果油气运移方向与水平方向夹角减小, 油气运移有效驱动功率将大幅减小(近似与sin2θ成正比), 导致油气藏总规模大幅增大。
| [1] |
HOUGHTON J C. Use of the truncated shifted Pareto distribution in assessing size distribution of oil and gas fields[J]. Mathematical Geology, 1988, 20(8): 907-937. |
| [2] |
POON D C, MCCORMACK M, THIMM H F. The application of fractal geostatistics to oil and gas property evaluation and reserve estimates[J]. The Journal of Canadian Petroleum Technology, 1993, 32(10): 24-27. |
| [3] |
BARTON C C, LA POINTE P R. Fractals in the earth sciences[M]. New York: Plenum Press, 1995: 13-33.
|
| [4] |
LAHERRERE J. Distribution of field sizes in a petroleum system: parabolic fractal, lognormal or stretched exponential?[J]. Marine & Petroleum Geology, 2000, 17(4): 539-546. |
| [5] |
曾怡. 分形法预测油气储量与资源量[J]. 石油实验地质, 1998(2): 152-154. ZENG Yi. A new method of petroleum resources estimation: fractal method[J]. Petroleum Geology & Experiment, 1998(2): 152-154. |
| [6] |
郭秋麟, 谢红兵, 米石云, 等. 油气资源分布的分形特征及应用[J]. 石油学报, 2009, 30(3): 379-385. GUO Qiulin, XIE Hongbing, MI Shiyun, et al. Fractal model for petroleum resource distribution and its application[J]. Acta Petrolei Sinica, 2009, 30(3): 379-385. |
| [7] |
刘晓冬, 徐景祯. 分形方法预测气田数量及其储量[J]. 石油学报, 2000, 21(2): 42-44. LIU Xiaodong, XU jingzhen. The number and reserves of gas fields are predicted by fractal method[J]. Acta Petrolei Sinica, 2000, 21(2): 42-44. |
| [8] |
陈新, 王绪龙, 靳涛. 石油储量分布的分形特征及其预测[J]. 新疆地质, 2001, 19(4): 297-299. CHEN Xin, WANG Xulong, JIN Tao. The fractal characteristic and its prediction of the distribution of oil reserves[J]. Xinjiang Geology, 2001, 19(4): 297-299. |
| [9] |
冯阵东, 戴俊生, 刘景东. 饶阳凹陷油藏储量在空间分布的分形特征[J]. 新疆石油地质, 2010, 31(4): 372-375. FENG Zhendong, DAI Junsheng, LIU Jingdong. Fractal characters of oil Reserves in spatial distribution in Raoyang Sag[J]. Xinjiang Petroleum Geology, 2010, 31(4): 372-375. |
| [10] |
宋宁, 王铁冠, 刘东鹰, 等. 分形方法在苏北盆地金湖凹陷石油资源评价中的应用[J]. 地质科学, 2006, 41(4): 578-585. SONG Ning, WANG Tieguan, LIU Dongying, et al. Application of fractal method predicating oil resources in the Jinhu Sag, North Jiangsu Basin[J]. Chinese Journal of Geology, 2006, 41(4): 578-585. |
| [11] |
鞠玮, 侯贵廷, 肖芳锋. 墨西哥湾盆地陆棚区油气田数量与储量规模的分形分析[J]. 北京大学学报(自然科学版), 2011, 47(6): 1049-1055. JU Wei, HOU Guiting, XIAO Fangfeng. Fractals of oil and gas field reserve distribution in outer continental shelf (OCS), Gulf of Mexico Basin[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2011, 47(6): 1049-1055. |
| [12] |
肖芳锋, 侯贵廷, 李乐, 等. 世界油气田规模分布的分形研究[J]. 应用基础与工程科学学报, 2011, 19(1): 95-103. XIAO Fangfeng, HOU Guiting, LI Le, et al. Fractal study on oil and gas field size distribution of the world[J]. Journal of Basic Science and Engineering, 2011, 19(1): 95-103. |
| [13] |
柳广弟, 孙明亮. 剩余压力差在超压盆地天然气高效成藏中的意义[J]. 石油与天然气地质, 2007, 28(2): 203-208. LIU Guangdi, SUN Mingliang. Significance of excess differential pressure in highly efficient gas accumulation in over-pressured basins[J]. Oil & Gas Geology, 2007, 28(2): 203-208. |
| [14] |
赵贤正, 蒋有录, 金凤鸣, 等. 富油凹陷洼槽区油气成藏机理与成藏模式:以冀中坳陷饶阳凹陷为例[J]. 石油学报, 2017, 38(1): 67-76. ZHAO Xianzheng, JIANG Youlu, JIN Fengming, et al. Hydrocarbon accumulation mechanism and model of sub-sags in hydrocarbon-rich sag: a case study of Raoyang sag in Jizhong depression[J]. Acta Petrolei Sinica, 2017, 38(1): 67-76. |
| [15] |
蒋有录, 万涛, 林会喜, 等. 成藏期剩余压力与储层排替压力下限耦合恢复油气成藏过程:以济阳坳陷车西洼陷为例[J]. 石油学报, 2011, 32(2): 265-272. JIANG Youlu, WAN Tao, LIN Huixi, et al. Reconstruction of hydrocarbon accumulation process by the matched relationship between surplus pressure and lower limit of reservoir displacement pressure in the hydrocarbon accumulation period: taking Chexi Sag in Jiyang Depression as an example[J]. Acta Petrolei Sinica, 2011, 32(2): 265-272. |
| [16] |
刘池洋, 张东东. 盆地复杂系统特征与研究思想和方法论[J]. 西北大学学报(自然科学版), 2009, 39(3): 350-391. LIU Chiyang, ZHANG Dongdong. Characteristics, thought of study and methodology of complex system of basin[J]. Journal of Northwest University(Natural Science Edition), 2009, 39(3): 350-391. |
| [17] |
彭少芳, 张昭. 线性和非线性非平衡态热力学进展和应用[M]. 北京: 化学工业出版社, 2006: 8-16.
|
| [18] |
曾丹苓. 工程非平衡热动力学[M]. 北京: 科学出版社, 1991: 102-125.
|
| [19] |
李如生. 非平衡态热力学和耗散结构[M]. 北京: 清华大学出版社, 1986: 127-160.
|
| [20] |
徐国宾, 练继建. 流体最小熵产生原理与最小能耗率原理(Ⅱ)[J]. 水利学报, 2003(6): 43-47. XU Guobin, LIAN Jijian. Theories of the minimum rate of energy dissipation and the minimum entropy production of flow (Ⅱ)[J]. Journal of Hydraulic Engineering, 2003(6): 43-47. |
| [21] |
赵丽娜, 徐国宾. 基于广义流和广义力的河流能耗率推导[J]. 天津大学学报(自然科学与工程技术版), 2015(12): 1126-1129. ZHAO Lina, XU Guobin. Derivation of energy dissipation rate of river based on generalized flux and generalized force[J]. Journal of Tianjin University(Science and Technology), 2015(12): 1126-1129. |
| [22] |
王铮. 利用耗散结构理论分析河道演变[J]. 地理科学, 1989, 9(2): 173-180. WANG Zheng. Analysis of river channel change with theory of dissipative structure[J]. Scientia Geographica Sinica, 1989, 9(2): 173-180. |
| [23] |
张学文. 组成论[M]. 合肥: 中国科学技术大学出版社, 2003: 176-182.
|
| [24] |
王志宏, 李建明. 饶阳凹陷异常高压与油气成藏关系[J]. 岩性油气藏, 2014, 26(6): 15-19. WANG Zhihong, LI Jianming. Abnormal high pressure and its relation to hydrocarbon accumulation in Raoyang Sag[J]. Lithologic Reservoirs, 2014, 26(6): 15-19. |
| [25] |
刘华, 张丰荣, 蒋有录, 等. 饶阳凹陷洼槽区地层压力特征及成因机制[J]. 中国石油大学学报(自然科学版), 2016, 40(4): 37-46. LIU Hua, ZHANG Fengrong, JIANG Youlu, et al. Characteristics and genetic mechanism of formation pressure in sags of Raoyang Depression[J]. Journal of China University of Petroleum(Edition of Natural Science), 2016, 40(4): 37-46. |
 2019,
Vol. 43
2019,
Vol. 43